Last year, our team announced a collection of discoveries and research milestones as part of our Scalability 2021 mission for Zcash. Our primary result was Halo, a new zk-SNARK that was finally capable of solving two outstanding issues in Zcash: removing the trusted setup while hitting performance targets and supporting a scalable architecture for private digital payments.
Our announcement came as a flurry of other discoveries were also published. By incorporating some of those ideas into Halo, we are able to achieve even more impressive performance gains. The next iteration of our work, which we call Halo 2, is a high-performance zk-SNARK implementation — written in Rust — which eliminates the need for a trusted setup while setting the stage for scalability in Zcash. Our goal is to build a robust and secure implementation that the Zcash community can feel confident adopting in the protocol.
Polynomial IOPs and the Inner Product Argument
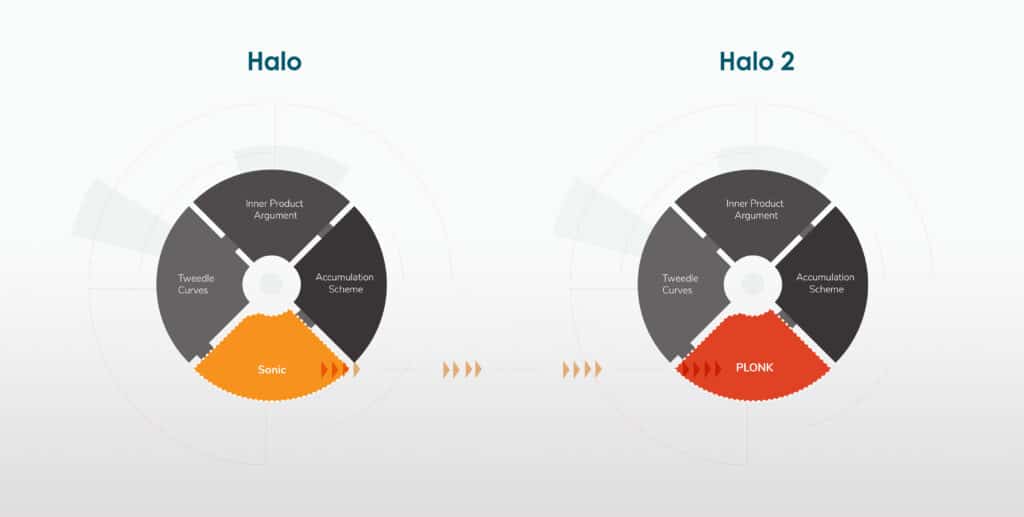
Last year, I co-authored a paper titled Sonic, where we introduced a new zk-SNARK protocol with some attractive new features. One of our accomplishments was to build our protocol based on two separable components: a “polynomial commitment scheme” and what is now known as a “Polynomial IOP,” which uses a polynomial commitment scheme to create zero-knowledge proofs for arbitrary computations.
There are a few polynomial commitment schemes described in the literature. The most efficient of them requires a trusted setup and was the focus of Sonic. However, a folklore technique for building a polynomial commitment scheme based on the inner product argument — famously used in Bulletproofs — did not require a trusted setup and had relatively small proof sizes, at the cost of poor verification performance.
In our Halo paper, we fully described this polynomial commitment scheme and realized that a special kind of aggregation technique existed in it that had not been spotted before. The technique allows a large number of independently created proofs to be verified nearly as quickly as verifying a single proof. This alone would offer a better alternative to our existing zk-SNARKs used in Zcash, depending on the use case.
Scalability and Recursion
Recursive proof composition allows a single proof to attest to the correctness of practically unlimited other proofs, effectively allowing a large amount of computation (and information) to be compressed. This is an essential component for scalable Zcash, not least because it allows us to horizontally scale the network while still allowing pockets of participants to trust the integrity of the remainder of the network.
Prior to Halo, achieving recursive proof composition required large computational expense and a trusted setup. One of our main discoveries was a technique we called “nested amortization,” which built on the aggregation technique mentioned above. This technique allowed us to achieve recursive composition using the polynomial commitment scheme based on inner product argument, massively improving on performance and avoiding the trusted setup.
Later, a team of scientists proposed a generalization of our approach called an “accumulation scheme” and proved its security. This new formalization exposes how our nested amortization technique actually works; by adding proofs to an object called an “accumulator,” where the proofs reason about the previous state of the accumulator, we can check that all previous proofs were correct (by induction) simply by checking the current state of the accumulator.
Efficient Polynomial IOPs
Halo described a concrete manifestation of recursive proof composition by stripping out the Polynomial IOP that was described in the Sonic paper and replacing the polynomial commitment scheme with one based on the inner product argument. Our discoveries allowed us to achieve recursive proof composition without a trusted setup, but it wasn’t as fast as we would have liked.
In parallel, many other teams were discovering new Polynomial IOPs that were more efficient than Sonic, such as Marlin. The most efficient of these new protocols is PLONK, which grants enormous flexibility in designing efficient implementations based on application-specific needs, essential for making a more efficient version of Halo.
Halo 2 for Zcash
Our goal for Halo 2 is to build something that is up to the community’s standards for inclusion in the Zcash protocol. We will not only incorporate new ideas that have emerged in the last year, but also aggressive optimizations and new tricks that our team discovers along the way, some of which we’re currently working hard to document and publish for the broader community.
